The Sine Wave
Figure. Single wavelength of a sine wave
The sine wave is the simplest waveform possible; it expresses a circle plotted over time. The above image shows a single wavelength of a sine wave (a transverse wave). One complete cycle is one compression and one rarefaction. This can be thought of a pushing a speaker cone forwards then back.
Figure 7. Twenty cycles of a sine wave produces a frequency of 20Hz, the lowest frequency we can hear.
¬
The ‘accepted’ frequency range of hearing of a young undamaged ear is 20Hz to 20kHz.
20 cycle per second = 20 Hertz (20Hz)
20,000 cycles per second = 20,000 Hertz (20kHz)
The sine wave is a pure tone and has zero harmonics. If you play a sine wave with a frequency of 1000Hz (1kHz) you’ll hear a continuing beep sound; if you play a sine wave at 40Hz you’ll hear pure sub bass. It is a ‘simple waveform’ (meaning that is a periodic (repeating) waveform.
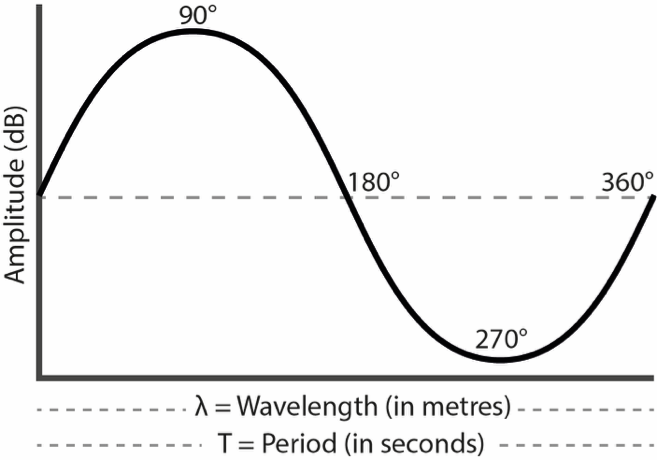
Figure 8: One wavelength of a sine wave
λ stands for lambda, which is the wavelength (in metres)

HIGHER FREQUENCY = shorter wavelength
![]()
LOWER FREQUENCY = longer wavelength
Quick tip: Sine waves produce pure tones with no harmonics, this means they are able to provide the purest sub bass of any waveform. All other waveforms introduce harmonics. Adding harmonics and changing their relative amplitues produces sounds with characteristic timbre (harmonic balance).
All other waveforms can be produced through adding sine waves together.
< Add simple waveform diagrams (labled with time as on p.49 of modern recording techniques) along with a complex waveform. >
The sine wave contains a fundamental frequency only, no harmonics
The sawtooth wave contains odd and even harmonics at inverse amplitudes.
The square wave contains only odd harmonics at inverse amplitudes
The triangle wave contains odd harmonics at inverse squared amplitudes. E.g. the third harmonic is 1/9 the amplitude of the fundamental (3×3=9)
Add dB and ‘harmonics’ to each graph
A sawtooth wave’s sound is harsh and clear and its spectrum contains both even and odd harmonics of the fundamental frequency